- Toate
- Teste cultura generala
- Teste psihologice
- Teste matematica
- Teste romana
- Teste anatomia omului
- Teste de botanica
- Teste filme
- Teste din istorie
- Teste de geografie
- Teste din astronomie
- Teste de logica
- Teste de chimie
- Teste de zoologie
- Teste despre desene animate
- Teste muzica
- Teste vedete
- Teste compatibilitate
- Mini-teste
- Teste haioase
- Teste fete
- Teste baieti
- Teste iubire
- Teste din referate pentru scoala
Afla ca sa stii
Jurnalul lui Aurel
De ce parintii fac pe politistul bun si politistul rau? Ai vazut probabil in filme cu politisti ca o echipa este formata din unul bun si unul rau. Si daca recunosti tiparul, sigur ti-ai dat seama...
› citeste mai multStiri
Bancul zilei
Care-i culmea fotbalului: Sa deschizi frigiderul si sa strigi:
Gooooooooool
Cultura generala
Melcii africani uriasi reprezinta cea mai mare specie de melci de pe planeta, avand cochilii ce pot creste pana la 30 de centimetri in lungime si 15 centimetri in diametru. Apetitul lor insatiabil pentru orice tip de plante si fructe ii transforma pe melcii uriasi in daunatori redutabili ai teritoriului in care se afla. Nu se dau in laturi de la a consuma nici macar tencuiala si vopseaua de pe peretii cladirilor.
› vrei mai multTest de logica cu conexiuni
Test greu despre Craciun

Shop Clopotel.ro

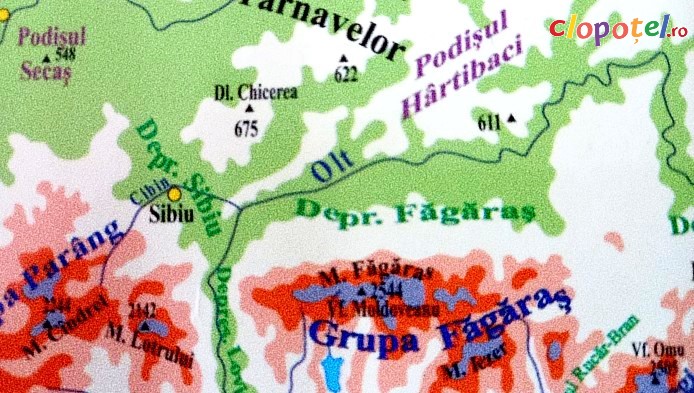
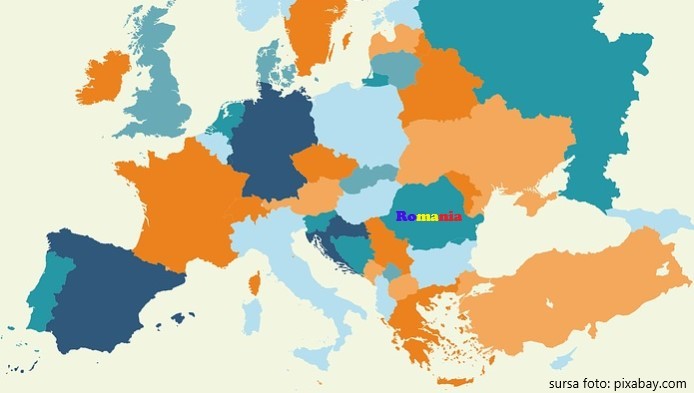
Test fulger despre geografia Romaniei nr. 8
Test fulger la istorie nr. 8